Modelling and Applications

Vision: The ModApp Group shall be a leading force in the performance and promotion of research on the use of mathematics in the natural sciences, social sciences, engineering and other disciplines.

Mission: As an academic group of the Institute of Mathematics, ModApp shall study mathematical models in the life and physical sciences, explore areas and create venues for the interdisciplinary use of mathematics in the natural sciences, social sciences, engineering, and other disciplines, and offer courses and services in promotion thereof.

Goals:

• To study and do research on mathematical models in the life and physical sciences from which can be gained insights on trends, causes and effects, solvability, stability, and, whenever possible, predictability
• To initiate research collaborations with the natural and social sciences, engineering, and other disciplines
• To participate in the discussion of public concerns that may benefit from ModApp expertise.

Areas of Research: Mathematical biology. Biochemistry. Epidemic spread and population dynamics. Dynamical systems. Network analysis.

• Research

  Modeling Biological Systems

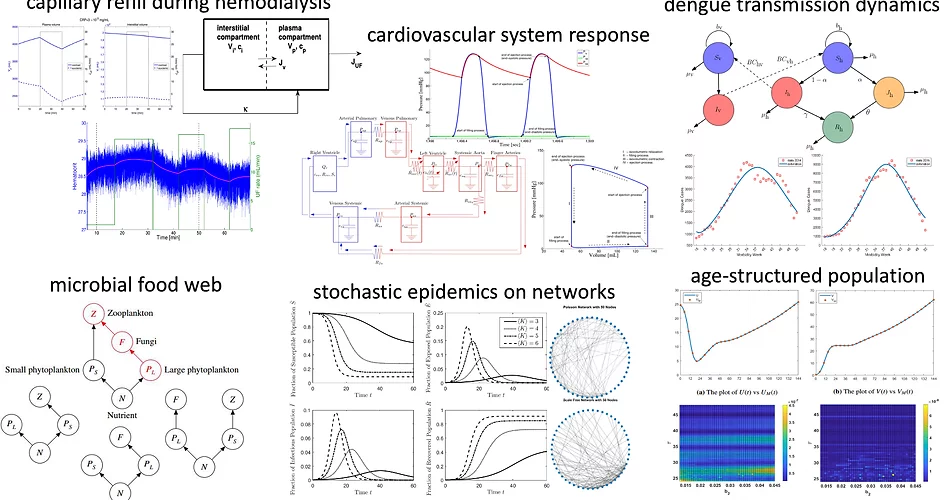  The use of mathematical models provides insights into the qualitative and quantitative characteristics of certain biological systems. Its complex behavior can be described by a set of nonlinear differential equations and its corresponding dynamics can be investigated through numerical simulations. Experimental measurements and observations are needed to validate the accuracy of model predictions.

  ModApp group is interested in quantifying complexities of physiological systems (e.g. cardiovascular-respiratory systems and capillary refilling); transmission dynamics of infectious diseases; theoretical modeling in ecology, stochastic epidemiology on random networks, and age-structured population.

  Chemical Reaction Network Theory

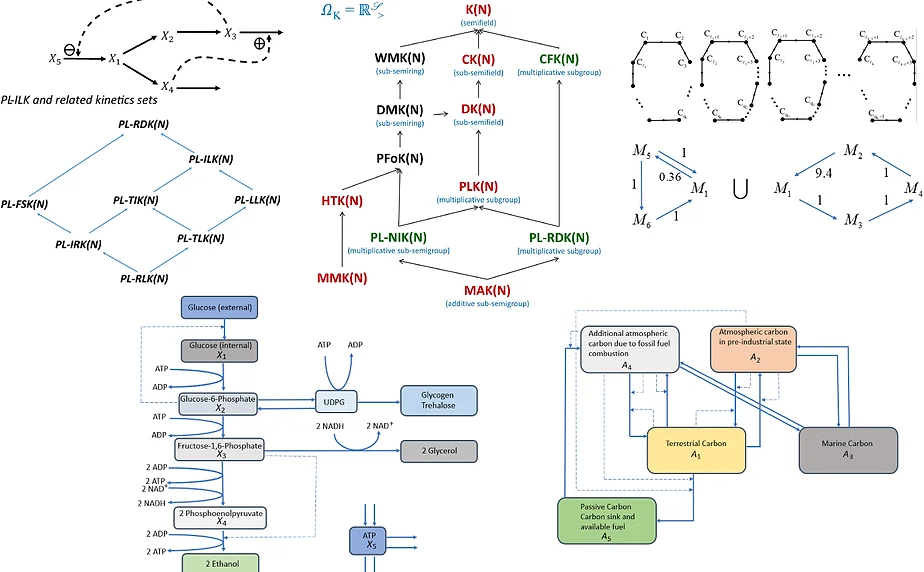  A chemical reaction network is a finite collection of chemical reactions that can be viewed as interactions among entities in a system. Kinetic functions are assigned to these reactions, and correspondingly, the dynamics of the kinetic system can be described by a system of ordinary differential equations (ODEs). The evolution of the concentrations of the chemical species over time can be captured by a system of ODEs. Chemical reaction network theory (CRNT) can be used to establish results on solutions of the ODEs such as existence, parametrization, uniqueness, multiplicity, and stability of steady states. One can also investigate persistence and permanence of systems, and periodicity of solutions. CRNT may also be used in cases where parameters are not specified and there are scarcity of kinetic order values.

  ​In the Philippines, a team of researchers lead by Dr. Eduardo R. Mendoza focuses on the existence and parametrization of steady states, multistationarity algorithms for classes of kinetics, and decomposition theory of chemical reaction networks. These results are being applied to areas such as systems biology, chemistry, game theory and engineering. Useful areas of mathematics to study CRNT are linear algebra, graph theory and differential equations for dynamical systems. There are also directions where one uses other areas such mathematical analysis.

  Applications of Optimal Control Theory in Biological Models

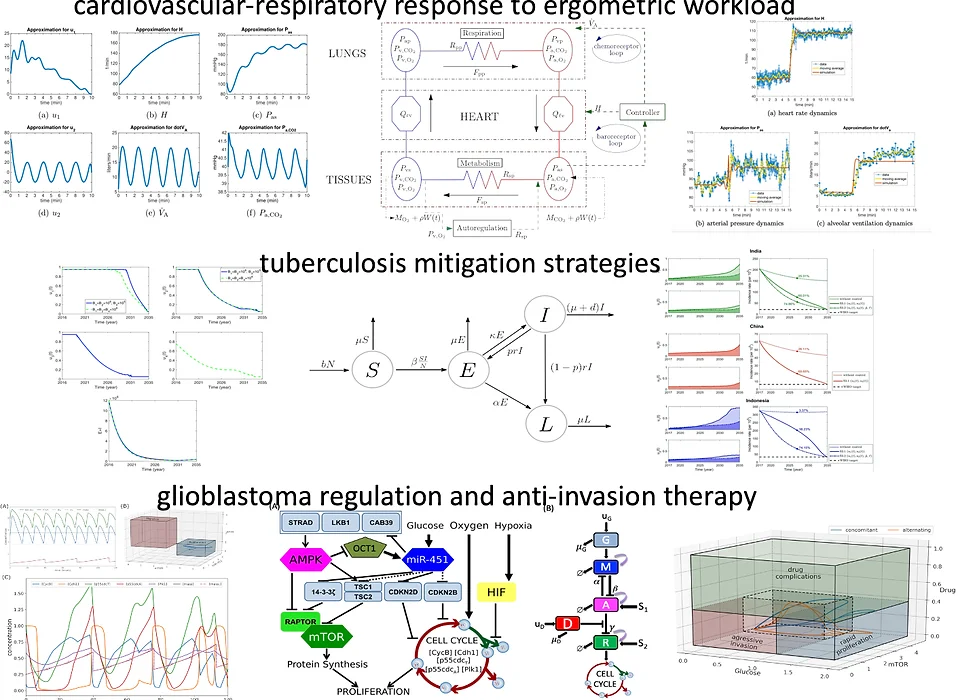  Optimal control theory is a branch of mathematics developed to obtain methods to control a dynamical system. It is a powerful tool that can be used to make informed decisions involving complex biological phenomena. In particular, it can be applied to determine effective and cost-efficient intervention measures to mitigate the spread of a disease. It can aid in the design of optimal therapeutic scheme in the treatment of lethal diseases like cancer.

  ​ModApp employs optimal control theory to describe the response of cardiovascular-respiratory system under ergometer test; examine optimal strategies to curtail transmission of infectious diseases (e.g. TB, HIV, etc.); and explore (poly)therapeutic strategies in cancer (e.g. glioblastoma, lung, etc.) treatment.

• Publications

  2023

  • Malaguit, J.C., Mendoza, V.M.P., Tubay, J.M. & Mata, M.A.E.  Identifying patterning behavior in a plant infestation of insect pests. Mathematical Biosciences (2023)
  • Hong, H, Hernandez, B.S., Kim, J. & Kim, J.K. Computational translation framework identifies biochemical reaction networks with special topologies and their long-term dynamics. SIAM Journal on Applied Mathematics 83:3, 1025-1048  (2023)
  • Monica, T., Tubay, J. & de los Reyes V, A.A. Quantitative assessment of a dual epidemic caused by tuberculosis and HIV  in the Philippines. Bulletin of Mathematical Biology 85, 56 (2023)
  • Lee, J., Mendoza, R., Mendoza, V.M.P., Lee, J., Seo, Y. & Jung, E. Modelling the effects of social distancing, antiviral therapy, and booster shots on mitigating Omicron spread. Scientific Reports 13, 6914 (2023)
  • Gavina, B.L.A., de los Reyes V, A.A., Olufsen, M.S., Lenhart, S. & Ottesen, J.T. Toward an optimal contraception dosing strategy. PLoS Computational Biology 19(4): e1010073 (2023)
  • Hernandez, B.S., Lubenia, P.V.N., Johnston, M.D. & Kim, J.K. A framework for deriving analytic long-term behavior of biochemical reaction networks. PLoS Computational Biology 19(4): e1011039 (2023)
  • Añonuevo, L.E., Lachica, Z.P.T., Amistas, D.A., Lato, J.I.E., Boniato, H.L.C., Catalan, J.M.G., Pasion, R.J.F., Yumang, A.P., Almocera, A.E.S., Arcede, J.P., Mata, M.A.E. & de los Reyes V, A.A. Transmission dynamics and baseline epidemiological parameter estimates of Coronavirus disease 2019 pre-vaccination: Davao City, Philippines. PLoS ONE 18(4): e0283068 (2023)

  2022

  • Hernandez, B.S. & Mendoza, E.R. Positive equilibria of power law kinetics on networks with independent linkage classes. J Math Chem (2022).
  • Escosio R.A.S. & Mendoza, R. A modified accelerated gradient descent using an n-dimensional golden section search for escaping saddle points. Proceedings of the 8th International Conference on Control and Optimization with Industrial Applications, Vol. 1, 24-26 August 2022, Baku, Azerbaijan, pp. 153-155
  • Mendoza, V.M.P., Mendoza, R., Ko, Y., Lee, J. & Jung, E. Managing bed capacity and timing of interventions: a COVID-19 model considering behavior and underreporting. AIMS Mathematics, 8(1): 2201-2225 (2023)
  • Ko, Y., Mendoza, V.M.P., Mendoza, R., Seo, Y., Lee, J. & Jung, E., Estimation of monkeypox spread in a non-endemic country considering contact tracing and self-reporting: a stochastic modeling study. J Med Virol, 1-11 (2022)
  • Cabanilla, K.I., Enriquez, E.A., Velasco, A.C., Mendoza, V.M.P. & Mendoza, R. Optimal selection of COVID-19 vaccination sites in the Philippines at the municipal level. PeerJ, 10:e14151 (2022)
  • Mendoza, V.M., Mendoza, R., Lee, J. & Jung, E. Adjusting non-pharmaceutical interventions based on hospital bed capacity using a multi-operator differential evolution. AIMS Mathematics, 7(11): 19922-19953 (2022)
  • Ko, Y., Mendoza, V.M., Mendoza, R., Seo, Y., Lee, J., Lee, J., Kwon, D., & Jung, E., Multi-Faceted Analysis of COVID-19 Epidemic in Korea Considering Omicron Variant: Mathematical Modeling-Based Study, J Korean Med Sci, 37(26):e209 (2022)
  • Ko, Y., Mendoza, V.M., Seo, Y., Lee, J., Kim, Y., Kwon, D., & Jung, E., Quantifying the effects of non-pharmaceutical and pharmaceutical interventions against COVID-19 epidemic in the Republic of Korea: Mathematical model-based approach considering age groups and the Delta variant, Math Model Nat Phenom, Forthcoming article (2022)
  • Hernandez, B.S. & Mendoza, E.R. Weakly reversible CF-decompositions of chemical kinetic systems, J Math Chem (2022)
  • de los Reyes V, A.A. & Kim, Y. Optimal regulation of tumour-associated neutrophils in cancer progression, R. Soc. Open Sci. 9: 210705 (2022)
  • Hernandez, B.S., Amistas, D.A., De la Cruz, R.J.L., Fontanil, L.L., de los Reyes V, A.A, & Mendoza, E.R. Independent, incidence independent and weakly reversible decompositions of chemical reaction networks, MATCH Commun Math Comput Chem 87(2): 367-396 (2022)

  ​2021

  • Ignacio, N., Liwag, R., Addawe, R. Spatiotemporal Analysis of Typhoid Cases in Baguio City, Philippines. In: Mohd, M.H., Misro, M.Y., Ahmad, S., Nguyen Ngoc, D. (eds) Modelling, Simulation and Applications of Complex Systems. CoSMoS 2019. Springer Proceedings in Mathematics & Statistics, vol 359. Springer, Singapore (2021)
  • Salonga, P.K.N., Mendoza, V.M.P., Mendoza, R.G., & Belizario Jr, V.Y. A mathematical model of the dynamics of lymphatic filariasis in Caraga Region, the Philippines. R. Soc. Open Sci. 8: 201965 (2021)
  • Calderon, P.G.B., Palma, Lean V., Kappel, F., & de los Reyes V, A.A. Control, Sensitivity and Identification of a Cardiovascular-Respiratory System Model. In: Mohd M.H., Misro M.Y., Ahmad S., Nguyen Ngoc D. (eds) Modelling, Simulation and Applications of Complex Systems. CoSMoS 2019. Springer Proceedings in Mathematics & Statistics, vol 359. Springer, Singapore. 151-173 (2021)
  • Hernandez, B.S. & De la Cruz, R.J.L. Independent decompositions of chemical reaction networks, Bull Math Biol 83, 1–23 (2021)
  • Hernandez, B.S. & Mendoza, E.R. Positive equilibria of Hill-type kinetic systems, J Math Chem 59, 840–870 (2021)
  • Aspirin, A.P., de los Reyes V, A. A. & Kim, Y. Polytherapeutic strategies with oncolytic virus–bortezomib and adjuvant NK cells in cancer treatment. J R Soc Interface 18: 20200669 (2021)
  • Magpantay, D. M., Hernandez, B. S., de los Reyes V, A. A., Mendoza, E. R. & Nocon, E. G. A Computational Approach to Multistationarity in Poly-PL Kinetic Systems, MATCH Commun Math Comput Chem 85(3): 605-634 (2021)
  • Hernandez, B. S. Analysis of Equilibria Properties of Chemical Reaction Networks with Independent Decompositions for Classes of Kinetics, MATCH Commun Math Comput Chem 85(3): 577-604 (2021)

  ​

  2020

  • ​Estadilla, C.D.S. & de los Reyes V, A.A. Optimal strategies for mitigating the HIV/AIDS epidemic in the Philippines. Math Meth Applied Sci 43: 10690-10710 (2020)
  • Jamilla, C.U., Mendoza, R.G. & Mendoza, V.M.P. Explicit solution of a Lotka-Sharpe-McKendrick system involving neutral delay differential equations using the r-Lambert W function. Math Biosci Eng 17(5): 5686-5708 (2020)
  • Jamilla, C.U., Mendoza, R.G., & Mező, I. Solutions of neutral delay differential equations using a generalized Lambert W function. Applied Mathematics and Computation, 382:125334 (2020)
  • Alota, C.P., Pilar-Arceo, C.P.C. & de los Reyes V, A.A. An edge-based model of SEIR epidemics on static random networks. Bull Math Biol 82, 96 (2020)
  • Kim, S., de los Reyes V, A.A. & Jung, E. Country-specific intervention strategies for top three TB burden countries using mathematical model. PLoS ONE 15(4): e0230964 (2020)
  • Cajayon, R.C., Lucilo, J.A., Pilar-Arceo, C.P.C. & Mendoza, E.R. Comparison of Two Nature-inspired Algorithms for Parameter Estimation of S-system Models. Philipp J Sci 149 (1): 63-78 (2020)
  • Hernandez, B. S. On the Independence of Fundamental Decompositions of Power-Law Kinetic Systems. MATCH Commun Math Comput Chem 84(1): 57-84 (2020)
  • Hernandez, B.S., Mendoza, E.R. & de los Reyes V, A.A. Fundamental Decompositions and Multistationarity of Power-Law Kinetic Systems. MATCH Commun Math Comput Chem 83(2): 403-434 (2020)
  • Hernandez, B.S., Mendoza, E.R. & de los Reyes V, A.A. A computational approach to multistationarity of power-law kinetic systems. J Math Chem 58, 56–87 (2020)

  ​​

  2019

  • ​Villar, J.J.S., Lubenia, P.V.N, Mendoza, E.R. & Pilar-Arceo, C.P.C. Structural Stability Analysis of Models of Dopamine Synthesis and D1 Receptor Trafficking in RPT Cells using CRNT. Philipp J Sci 148 (3): 523-533 (2019)
  • Pilar-Arceo, C.P.C., Jose, E.C., Lao, A.R. & Mendoza, E.R. Chemical Reaction Networks: Filipino Contributions to Their Theory and Its Applications. Philipp J Sci 148(2): 249-261​
  • Jung, E., de los Reyes V, A.A., Pumares, K.J.A. & Kim, Y. Strategies in regulating glioblastoma singling pathways and anti-invasion therapy. PLoS ONE 14(4): e0215547 (2019)
  • Almocera, A.E.S, Hsu, S.B. & Sy, P.W. Extinction and uniform persistence in a microbial food web with mycoloop: limiting behavior of a population model with parasitic fungi. Math Biosci Eng 16(1): 516-537 (2019)

  ​2018

  • ​de los Reyes V, A.A. & Escaner IV, J.M.L. Dengue in the Philippines: model and analysis of parameters affecting transmission. J Biol Dyn 12:1, 894-912 (2018)
  • Paguio, V.M.E., Kappel, F. & Kotanko, P. A model of vascular refilling with inflammation. Math Biosci 303: 101-114 (2018)
  • Jung, E., de los Reyes V, A.A., Pumares, K.J.A. & Kim, Y. Strategies in regulating glioblastoma singling pathways and anti-invasion therapy. PLoS ONE 14(4): e0215547 (2018)
  • Pilar-Arceo, C.P.P., Jose, E.C., Lao, A.R. & Mendoza, E.R. Reactant subspaces and kinetics of chemical reaction networks. J Math Chem 56: 395-422 (2018)
  • Talabis, D.A.S.J., Arceo, C.P.P. & Mendoza, E.R. Positive equilibria of a class of power-law kinetics. J Math Chem 56: 358-394 (2018)

  ​

  2017

  • ​Calderon, P.G.B., Habib, M., Kappel, F. & de los Reyes V, A.A. Control aspects of the human cardiovascular-respiratory system under a nonconstant workload. Math Biosci 289: 142-152 (2017)
  • Nazareno, A. L. & Hernandez, B.S. A mathematical model of the interaction of abscisic acid, ethylene and methyl jasmonate on stomatal closure in plants. PLoS ONE 12(2): e0171065 (2017)
  • Arceo, C.P.P., Jose, E.C., Lao, A.R. & Mendoza, E.R. Reaction networks and kinetics of biochemical systems. Math Biosci 283: 13-29

  ​

  2016

  • ​de los Reyes V, A.A., Fuertinger, D. H., Kappel, F., Meyring-Woesten, A., Thijssen, S. & Kotanko, P. A physiologically based model of vascular refilling during ultrafiltration in hemodialysis. J Theor Biol 390: 146-155 (2016)

  ​

  2015

  • ​Arceo, C.P.P., Jose, E.C., Marin-Sanguino, A. & Mendoza, E.R. Chemical reaction network approaches to biochemical systems theory. Math Biosci 269: 135-152 (2015)​
  • de los Reyes V, A.A., Jung, E., & Kim, Y. Optimal control strategies of eradicating glioblastoma cells after conventional surgery. J R Soc Interface 12: 20141392 (2015)
  • de los Reyes V, A.A. Dynamics of a cardiovascular model obtaining measurable pulsatile pressure output. World J Model Simul 11(1):20-32 (2015)

  ​

  2014

  • ​​de los Reyes V, A.A., Jung, E. & Kappel, F. Stabilizing control for a pulsatile cardiovascular mathematical model. Bull Math Biol 76(6):1306-1332 (2014)