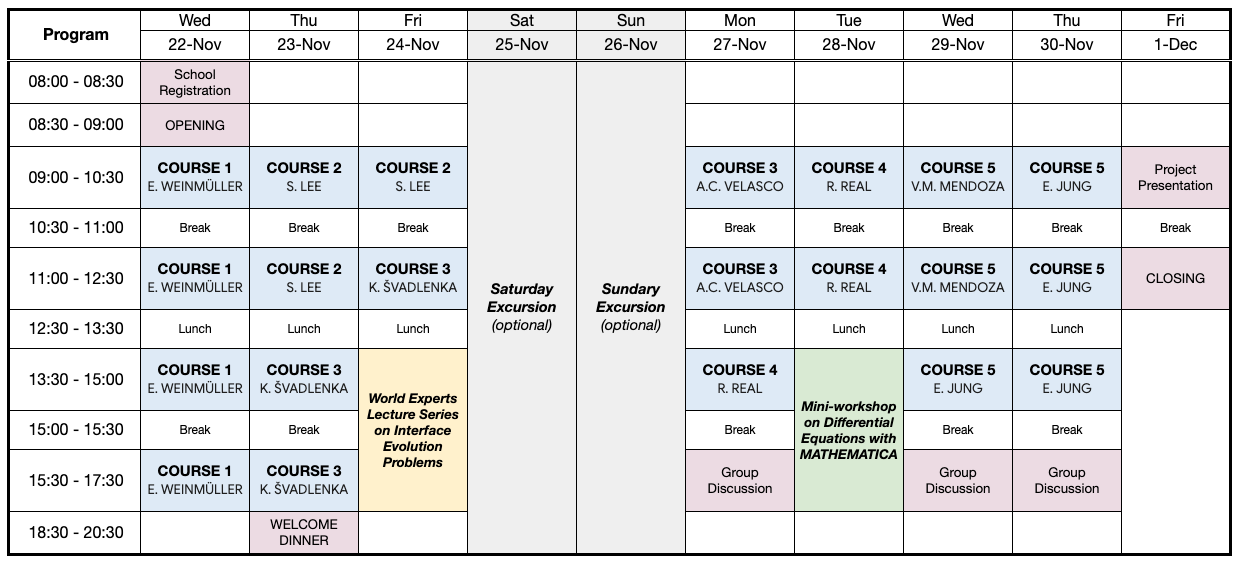
Schedule

Course 1

Numerical Solution of Singular BVPs in ODEs with Nonsmooth Data

We deal with boundary value problems (BVPs) for systems of ordinary differential equation (ODEs) with singularities. To compute the numerical approximation of the solution, we use polynomial collocation, because the method retains its high order even in case of singularities. We will discuss how the collocation performs for problems with unsmooth inhomogeneity. The updated version of the Matlab code bvpsuite1.1 will be implemented. For higher efficiency, estimate of the global error and adaptive mesh selection are provided. The code can be applied to arbitrary order problems in implicit form. We plan an introduction to the code and practical exercises.

Ewa Weinmüller, Ph.D.
Vienna University of Technology, Austria

Workshop Facilitators: Mered Wolde & Mathias Hohenegger

COURSE 2

Implicit representation of interface using PDEs

Interface problems (or multiphase problems) arise in various fields of science and engineering. However, it is a challenging problem in mathematics. The phase-field method is one of the most powerful methods for solving interface problems and it substitutes the boundary condition by a PDE of an auxiliary variable to capture the interfaces. In this talk, we discuss the mathematical background of the phase-field method, numerical schemes for the governing equations, and its applications.

Seunggyu Lee, Ph.D.
Division of Applied Mathematical Sciences,
Korea University, South Korea

COURSE 3

Finite element method for variational problems

This introductory course focuses on the numerical resolution of variational problems using the finite element method. In physical sciences and engineering, variational problems naturally arise from first principles and are intimately connected to partial differential equations. This two-part lecture series covers both the theoretical aspect of the finite element method and variational problems, and its numerical implementation using MATLAB and FreeFEM++.

COURSE 4

Introduction to Inverse Problems

Inverse problems appear across sciences. Here, from the observed effect or results, we determine the causes. The distinguishing property of inverse problems is ill-posedness, and this poses challenges in solving them. We motivate this course by presenting basic examples. Then we discuss the required mathematical background on Banach/Hilbert spaces, convex analysis and subdifferential calculus. The main part will be on regularization methods for linear inverse problems, such as Tikhonov regularization and Landweber iteration. We present their respective convergence analysis to illustrate the regularization property. Numerical examples, such as L1 and total variation regularization, will also be discussed.

Rommel R. Real, Ph.D.
Dept. of Math., Physics, and Computer Science,
University of the Philippines Mindanao, Philippines

COURSE 5

Data-fitting in epidemiological models

We give an introductory lecture on formulating models describing the transmission of infectious diseases among populations. Then, we present numerical optimization techniques to estimate model parameters from the available data. We discuss approaches to sensitivity and uncertainty analyses including partial rank correlation coefficient with Latin hypercube sampling and bootstrapping. Finally, we present applications to model the dynamics of infectious diseases such as COVID-19.

Workshop Facilitators: Jongmin Lee & Youngsuk Ko

WORLD EXPERTS LECTURE SERIES 2023

Details on WELS 2023 on Interface Evolution Problems can be accessed through this link: https://math.upd.edu.ph/wels2023/

MATHEMATICA MINI-WORKSHOP

Differential Equations with MATHEMATICA

The mini-workshop will introduce students to the basics of MATHEMATICA, with emphasis on its features as a symbolic algebra system. The main objective is to be able to use MATHEMATICA to symbolically solve differential equations and visualize the obtained solutions. Nevertheless, the talk will also introduce students to MATHEMATICA’s built-in functions that will enable them to numerically solve nonlinear and differential equations, and perform numerical integration and differentiation.

Jose Ernie C. Lope, Ph.D.
Institute of Mathematics,
University of the Philippines Diliman, Philippines

---

SEAMS SCHOOL 2023

Scientific Computing for Differential Equations and Applications
Institute of Mathematics, University of the Philippines Diliman
22 NOVEMBER 2023 — 01 DECEMBER 2023

---